Equation of state is used to derive variety of thermodynamic properties. This article illustrate calculation of specific heat ratio from Peng Robinson Equation of state.

Example

Calculate specific heat ratio ( γ = Cp/Cv ) for methane gas at 11 Bar & 300 °K. Critical constants for Methane are as following

• Critical temperature, Tc : 190.6°K
• Critical Pressure, Pc : 46.002 bar
• Accentric Factor, ω : 0.008

Ideal gas specific heat constants Cp^IG = A + B.T + C.T² + D.T³ are as following

• A = 4.5980
• B = 0.0125
• C = 2.86 x 10^-6
• D = -2.7 x 10^-9

where Cp is in cal/mol-K

Peng Robinson equation of state is defined as

 P = RT / (V - b)  - a / [V(V + b) + b(V - b)]

where

 ac = 0.45723553 R²Tc²/Pc
 b = 0.077796074 RTc/Pc
 m = 0.37464 + 1.54226ω - 0.26992ω² 
 a = ac[1 + m(1 - (T/Tc)0.5)]²

Above equation is translated into polynomial form and solved for values of Z using Newton-Raphson method.

 Z³ - (1 - B)Z² + Z (A - 2B - 3B²) - (AB - B² - B³) = 0
 Z = PV/RT
 A = aP/ (RT)²
 B = bP/ RT

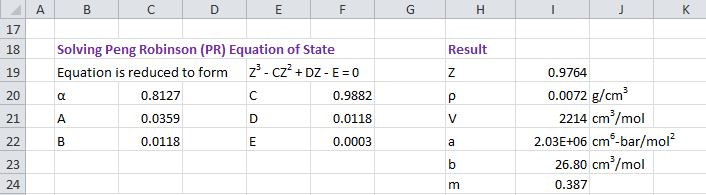
Following partial derivatives are required for calculating thermodynamic properties. First derivative is obtained by differentiation of P with respect to V at constant T.

 (δP/ δV)T = -RT/(v - b)² + 2a(v + b)/[v(v + b) + b(v - b)]²
 (δP/ δV)T = -0.00485 bar/(cm3/mol)

Second derivative is obtained by differentiation of P with respect to T at constant V.

 (δP/ δT)V = R/(v - b) - a'/[v(v + b) + b(v - b)]
 (δa/ δT)V = -mac/[(TTc)0.5(1 + m( 1 - (T/Tc)0.5))]
 (δP/ δT)V = 0.039 bar/K
 (δT/ δP)V = 25.814 K/bar

Third derivative is obtained by differentiation of V with respect to T at constant P.

 (δV/ δT)P = (R/P)[ T(δZ/δT)P + Z]
 (δZ/ δT)P = Num / Denom
 Num = (δA/δT)P (B-Z) + (δB/δT)P(6BZ+2Z-3B²-2B+A-Z²)
 Denom = 3Z&sup2 + 2(B-1)Z + (A-2B-3B²)

where,

 (δA/δT)P = (P/(RT)²)(a' - 2a/T)
 (δB/δT)P = -bP/(RT²)

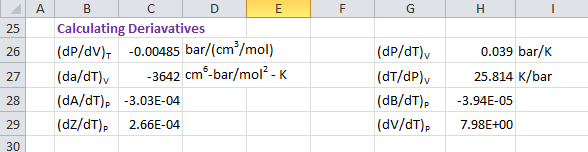
Calculation of Heat Capacities

Ideal gas heat capacity Cp^IG is calculated at 300 °K from polynomial equation provided above. Specific heat at constant volume for ideal gas, Cv^IG is calculated using following relation.

 CvIG = CpIG - R

Residual heat capacity at constant volume Cv ^R is calculated from internal energy U ^R as following.

 CvR = (δUR/δT)V
 UR = [(Ta'-a)/b(8)0.5] ln[(Z+B(1+20.5))/(Z+B(1-20.5))]
 CvR = [Ta"/b(8)0.5] ln[(Z+B(1+20.5))/(Z+B(1-20.5))]

where,

 a" = ac m (1 + m)(Tc/T)0.5/ (2TTc)

Specific heat capacity at constant pressure and volume is calculated using following equation.

 CpR = CvR + T(δP/δT)V(δV/δT)P - R
 Cp = CpIG + CpR
 Cv = CvIG + CvR

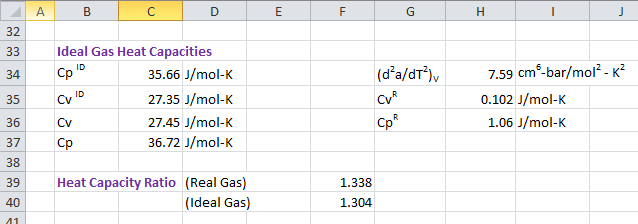
Specific heat ratio is obtained as :

 γ = Cp / Cv
 γ = 1.338

Resources

1. Spreadsheet for Specific heat ratio calculaton from Peng Robinson EOS