Equation of State are used to predict pure component and mixture properties such as compressibility, fugacity and mixture equilibrium.

Soave - Redlich - Kwong (SRK) EOS

Equation is defined as

 P = RT / (V - b)  - a α / V(V + b)

where

 a = 0.42748 R²Tc²/Pc
 b = 0.08664 RTc/Pc
 α = [1 + (0.48 + 1.574ω - 0.176ω² )(1 - Tr0.5)]²

Above equation is translated into polynomial form.

 Z³ - Z² + Z (A - B - B²) - AB = 0
 Z = PV/RT
 A = 0.42748 α Pr/ Tr²
 B = 0.08664 Pr/ Tr

where, Pr is Reduced Pressure (= P / Pc), Tr is Reduced Temperature (= T / Tc).

Newton-Raphson Method

Newton Raphson is an iterative procedure for finding roots of a function f(Z). Function f(Z) and its derivative f '(Z) is calculated. An initial guess is made for the root Z, successive vales for Z' are estimated using below relation till there is negligible difference between successive Z values.

 f(Z)  = Z³ - Z² + Z (A - B - B²) - AB
 f'(Z) = 3Z² - 2Z + (A - B - B²)
 Z'    = Z - f(Z)/f'(Z)

Example

Calculate compressibility factor for Methane based on SRK EOS at 30 bar, 285 °K. Critical parameters are Tc : 190.6 °K, Pc : 46 Bar, ω : 0.008.

Based on above equations f(Z) & f'(Z) is calculated as following.

 f(Z)  = Z³ - Z² + 0.0596 Z - 0.0037
 f'(Z) = 3Z² - 2Z + 0.0596

It is solved iteratively using Newton-Raphson method.

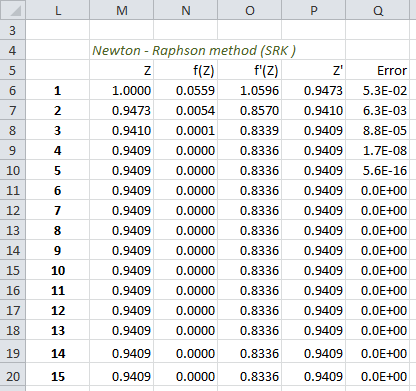
There is negligible error in successive values of Z after 6^th iteration.

 Z = 0.9409

Peng - Robinson (PR) EOS

Equation is defined as

 P = RT / (V - b)  - a α / [V(V + b) + b(V - b)]

where

 a = 0.45724 R²Tc²/Pc
 b = 0.07780 RTc/Pc
 α = [1 + (0.37464 + 1.54226ω - 0.26992ω² )(1 - Tr0.5)]²

Above equation is translated into polynomial form.

 Z³ - (1 - B)Z² + Z (A - 2B - 3B²) - (AB - B² - B³) = 0
 Z = PV/RT
 A = 0.45724 α Pr/ Tr²
 B = 0.07780 Pr/ Tr

where, Pr is Reduced Pressure (= P / Pc), Tr is Reduced Temperature (= T / Tc). Above relation is then solved for values of Z using Newton-Raphson method.

Resources

1. Spreadsheet for Solving cubic Equation of State