PT Flash calculation determines split of feed mixture F with a molar composition Zi, into Vapor V and Liquid L at pressure P and temperature T. These calculations can be done in a excel spreadsheet using Peng Robinson Equation of State (PR EOS). To start with bubble point pressure (PBubble) and dew point pressure (PDew) are determined for feed mixture.

• P < PDew, Mixture exists as super-heated vapor.
• P > PBubble, Mixture exists as sub-cooled liquid.
• PDew < P < PBubble, mixture exist in vapor and liquid phase.

Initial guess of vapor fraction V and Ki is made as following.

V = (PBubble - P)/(PBubble - PDew)
Ki = exp[ ln(Pc/P) + ln(10)(7/3)(1 + ω )(1-Tc/T)]

Based on initial Ki values, iteration is done to get value of V which satisfies material balance on system.

Yi = Ki.Xi
1 = V + L
Zi = V.Yi + L.Xi

where V & L are vapor and liquid fractions. Solving above equations for Xi gives :

Xi = Zi / ( V.( Ki - 1) + 1 )

At Flash conditions

Σ Yi - Σ Xi = 0

Above equation can be solved by iteration using Newton Raphson method. Function F(V) is defined as:

F(V) = Σ Yi  - Σ Xi
F(V) = Σ [Zi (Ki - 1)/( V.(Ki - 1) + 1)]

Derivative of F(V) is calculated as:

F'(V) = Σ -[Zi(Ki - 1)² /( V.(Ki - 1) + 1)²]

New estimate of vapor fraction is calculated as:

V New = V - F(V)/F'(V)

Function F(V) and F'(V) are calculated based on new vapor fraction and this process is repeated till there is negligible difference in between V and V_New. Vapor fraction thus obtained is then used to estimate vapor and liquid molar composition (Yi & Xi).

Iteration for Ki

Vapor (Yi) and Liquid (Xi) mol fractions estimated above are used to generate values for Ki. Parameters for Peng Robinson EOS are calculated for each component i.

κi = 0.37464 + 1.54226ω - 0.26992ω²
αi = [ 1 + κi (1 - (T/Tc)0.5)]²
ai = 0.45724 (RTc)²α / Pc
bi = 0.07780 RTc / Pc

φ_i^L Calculation

Mixture parameters are calculated.

aij = [(ai.aj)0.5(1 - kij)] = aji
a = ΣiΣj aij.Xi.Xj
b = Σi bi.Xi
A = aP/(RT)²
B = bP/RT

where, kij's are Binary Interaction Parameter available from literature. Following cubic equation is solved to get Z^L.

Z³ + (B-1)Z² + (A-3B² -2B)Z + (B³+B²-AB) = 0

Roots calculated are arranged in descending order, highest root gives Z^V and lowest root gives Z^L.

Based on Z^L, liquid fugacity φ_i^L is calculated for each component.

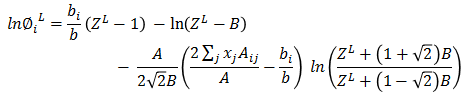
φ_i^V Calculation

Mixture parameters are calculated.

a = ΣiΣj aij.Yi.Yj
b = Σi bi.Yi
A = aP/(RT)²
B = bP/RT

Cubic equation is solved to get Z^V.

Z³ + (B-1)Z² + (A-3B² -2B)Z + (B³+B²-AB) = 0

Based on Z^V, vapor fugacity φ_i^V is calculated for each component.

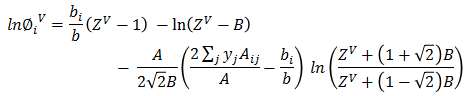
Ki is calculated as:

Ki = φiL/φiV

New values of Ki thus calculated are again used to estimate V and thereafter Xi & Yi. Iteration is repeated till there is no further change in Ki values. Typically, in 10 iterations change in Ki values become negligible.

Resources

1. Spreadsheet for PT Flash calculation using PR EOS