Non-Newtonian fluids occur commonly in our world. Power law model is applicable for time independent non-Newtonian fluids and can be written as

τ = K γn

where, τ is shear stress, γ is shear rate, K is called flow consistency index and n is called flow behavior index.

For n < 1, the apparent viscosity decreases with increasing shear rate and fluid is called pseudoplastic or shear-thinning. A majority of non-Newtonian fluids like polymer solutions, pulp suspensions, pigments and food materials can be found in this category.

For n > 1, the apparent viscosity increases with shear rate increase and fluid is termed dilatant or shear-thickening. Examples are starch and clay suspensions in water.

For n = 1, Newtonian flow behavior is expected.

Reynolds number for the power law fluid is defined as

where, D is pipe inside diameter, V is fluid velocity and ρ is fluid density.

For Re < 2100, flow is laminar and friction factor is calculated as

f = 16 / Re

For turbulent flow, following relationship was developed by Dodge and Metzner.

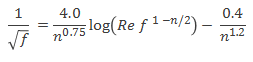
Pressure drop is calculated as

ΔP = 2fρV² (L'/D)

L' = L + Le

where, L is the pipe length and Le is equivalent length due to loss in pipe fittings and is calculated as

Le = kD / 4f

Resources

1. Web based calculation available at checalc.com
2. Spreadsheet for Power Law Fluid Flow

References

1. Fluid friction at Petrowiki
2. Chemical Engineering Fluid Mechanics, Ron Darby, 2^nd Edition