Linear Programming is a widely used mathematical technique designed to help managers and engineers in planning and decision making relative to resource allocation. Linear programming (LP) model essentially consists of 3 components.

• Decision Variables

• Objective function

• Constraints

This article shows how to develop LP model in Excel.

Example

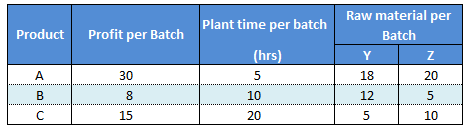
Multipurpose plant is used to manufacture three products A, B and C from raw materials Y and Z. Amount of raw materials required, batch times and profits per batch are shown as below. Determine number of batches to be processed every week for each product to maximize the profit. Plant is operating for 150 hours per week. Raw material available per week is Y : 216 units and Z : 200 units.

Decision Variables

Number of batches for each product X_A , X_B and X_C

Objective Function

Maximize profit for production.

 Maximize ( 30 XA + 8 XB + 15 XC)

Constraints

Total time available for production.

 5 XA + 10 XB + 20 XC <= 150

Raw material Y available for production.

 18 XA + 12 XB + 5 XC <= 216

Raw material Z available for production.

 20 XA + 5 XB + 10 XC <= 200

Excel Solver

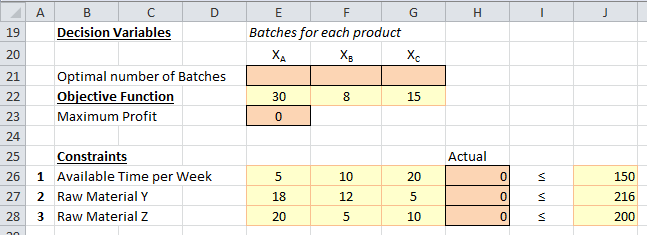
Identify Cells E21,F21,G21 which hold values of decision variables. Calculate objective function in cell E23 as following.

 =SUMPRODUCT(E22:G22,E21:G21)

Identify Cells H26,H27,H28 to hold values of constraints.

 Cell H26  =SUMPRODUCT(E26:G26,$E$21:$G$21) 
 Cell H27  =SUMPRODUCT(E27:G27,$E$21:$G$21)
 Cell H28  =SUMPRODUCT(E28:G28,$E$21:$G$21)

Click "Solver" in Data ribbon (Excel 2010) and fill data as in below screenshot.

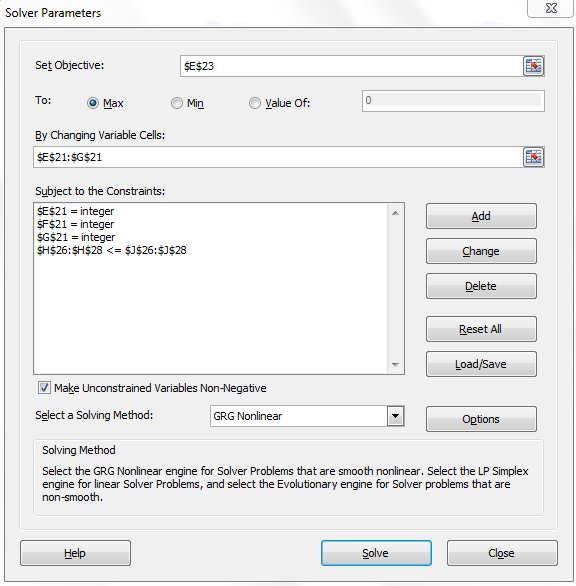
Add constraints by clicking "Add" Button. Number of batches needs to be integer, click on add constraint and select cell E21, F21, G21 and select "Int" to make these variable integer. After adding constraints click Solve to get results.

 XA = 8
 XB = 4
 XC = 2
 Profit = 302

Example

A refinery has four type of crude oils available that have the yields shown in the following table. Because of maximum demand, production of gasoline, heating oil, jet fuel and lube oil must be limited as shown in the table. Find the optimum weekly requirement of crude oils to maximize the refinery profit.

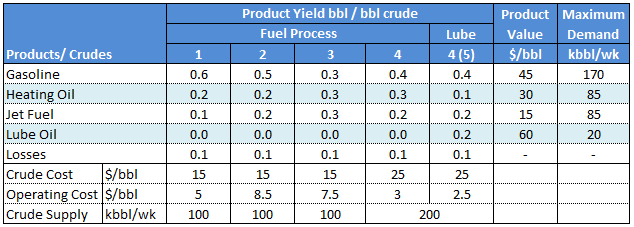
Profit from crude oil 1 is obtained by adding value of products formed and subtracting crude and operating cost.

 Crude 1 Profit = 45(0.6) + 30(0.2) + 15(0.1) - (15 + 5) = 14.5 k$

Similarly profits of 8.0, 4.5, 2.0, 8.5 k$ for crude options 2,3,4,5.

Decision Variables

Weekly crude oil requirement X1, X2, X3, X4 and X5

Objective Function

Maximize refinery profit.

 Maximize ( 14.5 X1 + 8 X2 + 4.5 X3 + 2 X4 + 8.5 X5)

Constraints

Limits on production of gasoline, heating oil, jet fuel and lube oil.

 0.6 X1 + 0.5 X2 + 0.3 X3 + 0.4 X4 + 0.5 X5 <= 170
 0.2 X1 + 0.2 X2 + 0.3 X3 + 0.3 X4 + 0.1 X5 <= 85
 0.1 X1 + 0.2 X2 + 0.3 X3 + 0.2 X4 + 0.2 X5 <= 85
 0.2 X5 <= 20

Limits on availability of crude oils.

 X1 <= 100
 X2 <= 100
 X3 <= 100
 X4 + X5 <= 200

Define the problem in excel solver and get following results.

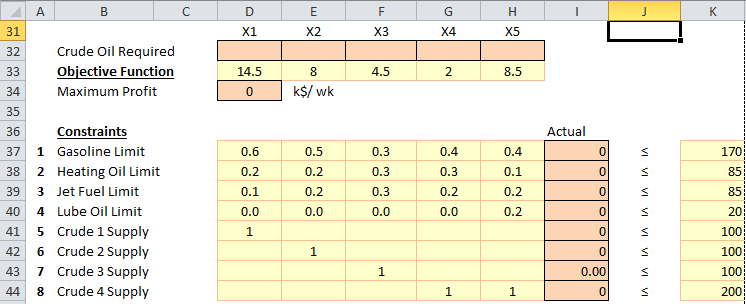
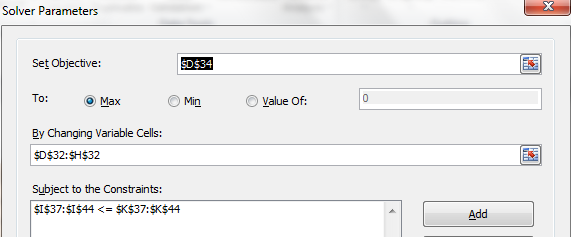
 X1 = 100
 X2 = 100
 X3 = 66.67
 X4 = 0
 X5 = 100
 Profit = 3400 k$/wk

Resources

1. Spreadsheet for above examples on linear programming