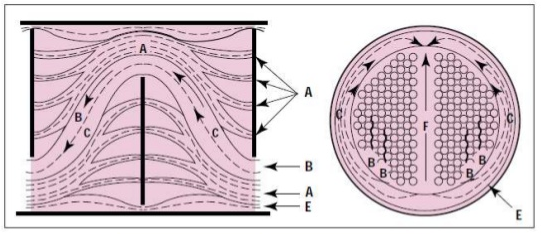
In Bell Delaware method, the fluid flow in the shell is divided into a number of individual streams. Each of these streams introduces a correction factor which is used to correct heat transfer coefficient and pressure drop across the shell. This article gives step-by-step guidance on doing heat exchanger rating analysis based on Bell-Delware method.

Shell Side Heat Transfer Coefficient, h_s

Cross flow area, S_m is the minimum flow area in one baffle space at the center of the tube bundle. It is calculated by following equation:

Sm = B[(Ds - DOTL) + (DOTL - Do)(PT - Do)/PT,eff ]

where, P_T is tube pitch, B is central baffle spacing, D_OTL is outer tube limit diameter, Ds is shell diameter and Do is tube outside diameter.

PT,eff = PT for 30° and 90° layouts
PT,eff = 0.707*PT for 45° layout

Shell side cross flow mass velocity, G_S is defined as:

GS = mS/Sm

where, m_S is shell side mass flow rate. Shell side Reynolds number Re_S is then calculated from

ReS = Do.GS / μS

where, μ_S is the shell side fluid dynamic viscosity at average bulk temperature.

Shell side Prandtl number Pr_S is calculated as following :

PrS = CP,S.μS / kS

where, C_P,S is the shell side fluid specific heat and k_S is the shell side fluid thermal conductivity.

Colburn j-factor for an ideal tube bank is defined as:

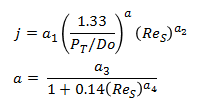
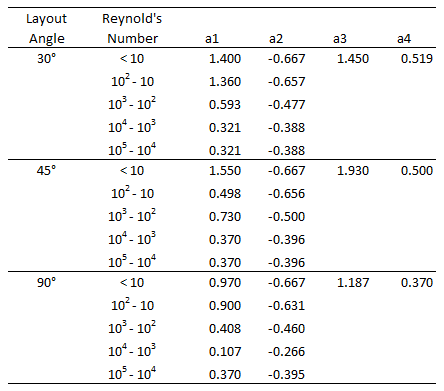
where a1, a2, a3 and a4 are correlation constants listed below.

The ideal tube bank based coefficient is calculated from -

where, μ_S,W is shell side fluid viscosity at wall temperature.

Correction factor for Baffle Window Flow, J_C

The factor J_C accounts for heat transfer in the baffle windows. It has a value of 1.0 for exchanger with no tubes in the windows.

JC = 0.55 + 0.72FC
FC = 1 - 2FW
FW = (θCTL - Sin(θCTL))/2π
θCTL = 2cos-1(Ds(1 - 2*Bc/100)/DCTL)
DCTL = DOTL - Do

where, Bc is segemental baffle cut in %.

Correction factor for Baffle Leakage, J_L

The correction factor J_L considers the effects of the tube-to-baffle and shell-to-baffle leakage streams on heat transfer.

JL = 0.44(1-rS) + (1-0.44(1-rS))exp(-2.2rL)
rS = Ssb /(Ssb + Stb)
rL = (Ssb + Stb)/ Sm
Ssb = Ds*DSB(π - 0.5θDS)
Stb = (π/4)((Do+LTB)2 - Do2)Nt(1-FW)
θDS = 2cos-1(1 - 2Bc/100)

where, Nt is number of tubes, D_SB is diametral clearance between shell & baffle and L_TB is diametral clearance between tube and baffle.

Correction factor for Bundle Bypass effects, J_B

Bundle bypass correction factor J_B accounts for the bundle bypass stream flowing in the gap between the outermost tubes and the shell. The number of effective rows crossed in one cross flow section, N_tcc between the baffle tips is provided by following equation.

Ntcc = (Ds/Pp)(1 - 2Bc/100)
Pp = PT 30.5/2 for 30° layout
Pp = PT / 20.5 for 45° layout
Pp = PT for 90° layout

Ratio of sealing strips to tube rows r_ss is provided by

rss = Nss/ Ntcc

where N_ss is number of sealing strips (pairs) in one baffle.

The bundle bypass flow area, S_b is defind as

Sb = B(Ds - DOTL - Do/2)

where, B is central baffle spacing. Correction factor J_B is then calculated as following -

JB = exp(-Cj(Sb / Sm)(1 - (2rss)1/3)) for rss < 0.5
JB = 1 for rss >= 0.5
Cj = 1.35 for ReS < 100
Cj = 1.25 for ReS >= 100

Correction factor for adverse temperature gradient, J_R

The factor J_R accounts for the decrease in the heat transfer coefficient with downstream distance in laminar flow.

Ntcw = (0.8/Pp)(Ds(Bc/100) - (Ds-(DOTL-Do))/2 )
NB = 1 + (int)(L - 2Ls - LBIn - LBOut)/B
NC = (Ntcw + Ntcc)(1 + NB)
JRL = (10/NC)0.18
JR = 1, ReS > 100
JR = JRL + (20-ReS)(JRL - 1)/80, ReS <= 100, ReS > 20
JR = JRL, ReS <= 20

where, L is tube length, Ls is tubesheet thickness, LB_In is inlet baffle spacing and LB_Out is outlet baffle spacing.

Correction factor for unequal baffle spacing, J_S

n1 = 0.6, ReS >= 100
n1 = 1/3, ReS < 100
JS = ((NB-1)+(LBIn/B)1-n1 + (LBOut/B)1-n1)/((NB-1)+(LBIn/B) + (LBOut/B))

Shell side heat transfer coefficient is calculated as

hs = hIdeal(JC.JL.JB.JS.JR)

Shell Side Pressure Drop, ΔP_s

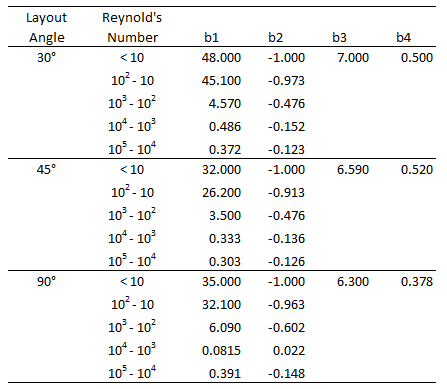
Friction factor for ideal tube bank is calculated as following -

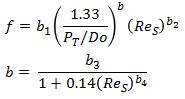
where b1, b2, b3 and b4 are correlational constants listed below.

Pressure drop for an ideal tube bank is calculated from

ΔPIdeal = 2f(GS²/ρS)(μS/μS,W)0.14 Ntcc

Correction factor for Baffle Leakage, R_L

RL = exp(-1.33(1+rS)rLp)
p = 0.8 - 0.15(1+rS)

Pressure drop for window section, ΔP_W

Following terms are calculated as -

SWG = (Ds²/8)(θDS - Sin(θDS))
SWT = Nt.FW(πDo²/4)
SW = SWG - SWT
GW = mS/(Sm.SW)0.5
DW = 4.SW /(π.Do.Nt.FW + θDS.Ds)

Pressure drop for laminar and turbulent flow is calculated.

ΔPW, Turb = NB.RL(2+0.6*Ntcw).GW²/(2.ρS)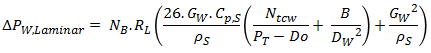

ΔPW = ΔPW, Turb , ReS >= 100
ΔPW = ΔPW,Laminar , ReS < 100

Correction factor for Bundle Bypass effect, R_B

RB = exp(-Cr(Sb / Sm)(1 - (2rss)1/3)) for rss < 0.5
RB = 1 for rss >= 0.5
Cr = 4.5 for ReS < 100
Cr = 3.7 for ReS >= 100

Correction factor for unequal baffle spacing, R_S

n = 0.2, ReS >= 100
n = 1.0, ReS < 100
RS = 0.5((B/LBIn)2-n + (B/LBOut)2-n)

Pressure drop in Central Baffle spaces, ΔP_C is defined as -

ΔPC = (NB - 1)ΔPIdeal.RL.RB

Pressure drop in entrance & exit baffle spaces, ΔP_E is calculated as -

ΔPE = ΔPIdeal(1 + Ntcw/Ntcc).RB.RS

Shell side pressure drop is calculated as following -

ΔPS = ΔPW + ΔPC + ΔPE

Tube Side Heat Transfer Coefficient, h_t

Reynold's number and Prandtl number are calculated as following -

ReT = Di.v.ρt/μt
PrT = Cp,t.μt/kt

where, Di is tube inside diameter, v is velocity, ρ_t is density, μ_t is viscosity, k_t is thermal conductivity and C_p,t is specific heat for fluid on tube side.

For laminar flow, Re_T < 2300, Sieder and Tate correlation is used for Nusselt's nubmer.

Nu = 1.86(ReT.PrT.Di/Leff)1/3
Leff = L - 2*Ls

For turbulent flow, Re_T > 10,000, following equation developed by Petukhov-Kirillov can be used.

Nu = (f/2)ReT.PrT/(1.07+12.7(f/2)0.5(PrT2/3-1))
f = (1.58 ln(ReT) - 3.28)-2

For transient flow, Nusselt number can be interpolated from Nu _Laminar & Nu _Turbulent.

Heat transfer coefficient is calculated as following -

ht = Nu.(kt/Di)(μt/μt, w)0.14

Tube Side Pressure Drop, ΔP_t

Tube side pressure drop is calculated by following equation -

ΔPt = (4.f.Leff.Np/Di + 4.Np)ρt.v²/2

where, Np is number of tube passes.

Overall Heat Transfer Coefficient, U

Resistance due to tube wall is calculated as following

Rtube = Do/(2.ln(Do/Di).ktube)

where, k_tube is thermal conductivity of tube material. Overall clean heat transfer coefficient, U_Clean is calculated as per below equation

UClean = 1/(hS + Do/(Di.ht) + Rtube)

Overall dirty heat transfer coefficient, U_Dirty is calculated as per below expression

UDirty = 1/(1/UClean + fshell + ftube)

where, f_shell & f_tube are fouling factors for shell and tube side.

Heat transfer coefficient required, U_Required is calculated as following

URequired = Q /(A x LMTDcorrected)

where, Q is heat duty, A is heat transfer area and LMTD_corrected is corrected logarithmic mean temperature difference.

Over Surface, % = (UClean/URequired - 1)*100
Over Design,  % = (UDirty/URequired - 1)*100

Resources

1. Web based calculation available at checalc.com
2. Spreadsheet for Heat Exchanger Rating based on Bell-Delaware Method

References

1. Chapter 4, Design Fundamentals of Shell-And-Tube Heat Exchanger
2. Process Heat Transfer - Principles and Applications, 2007 - Robert W. Serth
3. Chemical Process Computations, 1985 - Raghu Raman