This article illustrates determination of terminal velocity required for gravity separation. Performing a force balance on liquid droplet settling out of gas stream results in following relationship.

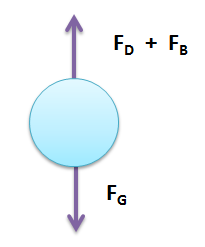
where F_B is force due to Buoyancy, F_D is force due to Drag and F_G is force due to gravity.

 FG = m.g
 FB = m.ρV.g/ρL
 FD = CD.(ρV.Vt²/2).AP

Assuming spherical liquid droplet with diameter D_P, above equation gets reduced to

 FD = FG - FB
 FD = CD.(ρV.Vt²/2).(π.DP²/4)
 FG - FB = m.g(ρL - ρV)/ρL
 m = 4/3.(π.DP³/8).ρL

Balancing above equation gives following relation for terminal velocity V_t.

 Vt = [(4gDP/ 3CD).(ρL - ρV)/ρV ]0.5

Drag coefficient depends on shape of particle and Reynold's number and can be determined from below graph.

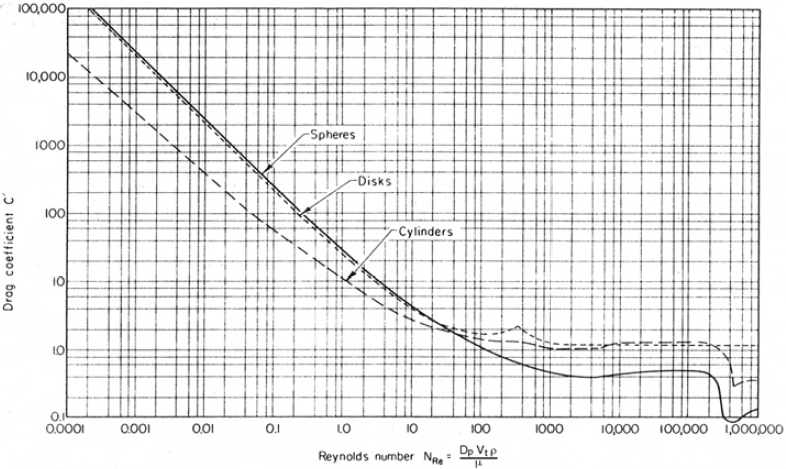
Above curve can be simplified into 3 sections resulting into 3 settling laws.

Stoke's Law

At low Reynold's number < 2, a linear relationship exists between C_D and Re.

 CD = 24/Re
 Re = DP.ρV.Vt/μV
 Vt = g.DP².(ρL - ρV)/18μV

In English units, with D_P in feet, V_t in feet/sec, ρ in lb/ft³, g = 32.2 feet/sec² and μ in centipoise, above equation can be expressed as.

 Vt = 1488.g.DP².(ρL - ρV)/18μV

Criterion K is defined to determine the flow regime as following.

 K = DP[g.ρV(ρL - ρV)/μV²]1/3

Value of K is evaluated for Reynold's number 2 based on Stoke's Law.

 Re = 2
 Vt = 2.μV/(ρV.DP)
 K = (36)1/3
 K = 3.3

For K < 3.3 Stoke's Law is applicable.

Intermediate Law

For 2 < Re < 500, Intermediate law applies.

 CD = 18.5/Re0.6
 Vt = 0.153 g 0.71 DP 1.14 (ρL - ρV)0.71/ ( ρV0.29. μV0.43)

In English units, with viscosity in centipoise, above equation can be expressed as

 Vt = 3.49 g 0.71 DP 1.14 (ρL - ρV)0.71/ ( ρV0.29. μV0.43)

Newton's Law

Newton's law is applicable for Reynold's number in range of 500 to 200,000.

 CD = 0.44
 Vt = 1.74 (g.DP(ρL - ρV)/ ρV)0.5

Value of K is evaluated for Reynold's number 500 based on Newton's Law.

 Re = 500
 K = (500/1.74)2/3
 K = 43.5

For K in the range of 3.3 to 43.5, Intermediate Law is applicable; for K > 43.5, Newton's Law is applied.

Stoke's Law is applicable for vapor separation from a continuous liquid phase and dispersed liquid separation from a continuous liquid phase. Intermediate Law is typically used for liquid separation from a continuous vapor phase.

Example

Calculate diameter for a vertical vapor liquid separator based on gravity separation. Gas flowrate is 50,000 lb/h, density is 3.7 lb/ft³ and viscosity is 0.01 cP. Liquid flowrate is 12,000 lb/h, density is 51.5 lb/ft³ and viscosity is 0.42 cP. Assume liquid particle diameter D_PL as 250 micron and vapor particle diameter D_PV as 150 micron.

Terminal velocity is to be calculated for gravity settling of liquid droplet from vapor phase. K Value is calculated to determine the applicable flow regime.

 K = 41.1

Intermediate Law is applicable for this case. Terminal velocity is calculated based on Intermediate Law.

 Vt = 0.96 feet/sec

Margin of 75% is taken on terminal velocity and vessel diameter is calculated.

 D1 = 2.58 feet

A second terminal velocity is calculated for disentraining vapor from liquid phase. Typically Stoke's law is applicable for vapor disentrainment. Terminal velocity is calculated based on Stoke's law.

 Vt = 0.07 feet/sec

With margin of 75% on terminal velocity, vessel diameter is calculated.

 D2 = 1.22 feet

Comparing both diameter values, highest value of 2.58 feet is selected as a minimum diameter required for gravity separation of vapor and liquid.

Resources

1. Spreadsheet for Determining diameter of Vertical Vapor Liquid Separator based on Gravity Separation