This article shows how to estimate binary interaction parameter (BIP) used in Peng Robinson (PR) Equation of State (EOS) from experimental data by regression in excel spreadsheet.

Example

Determine binary interaction parameter used in Peng Robinson EOS for a mixture of acetone and chloroform from Tx-y experimental data available at 101.33 kPa.

Obtain pure component properties like critical temperature (Tc), critical pressure (Pc) and accentric factor ω from literature. Experimental K1 is determined from x, y data.

K1Experimental = y1 / x1

Peng Robinson EOS parameters are calculated.

κi = 0.37464 + 1.54226ω - 0.26992ω²
αi = [ 1 + κi (1 - (T/Tc)0.5)]²
ai = 0.45724 (RTc)²α / Pc
bi = 0.07780 RTc / Pc

Mixture parameters are calculated next

a12= [(a1.a2)0.5(1 - k12)] = a21
a = a1.x1² + 2.a12.x1.x2 + a2.x2²
b = b1.x1 + b2.x2
A = aP/(RT)²
B = bP/RT

where k12 is Binary Interaction Parameter (BIP) to be estimated. For first run, use a guess value to start calculation.

Following cubic equation is solved to get Z^L.

Z³ + (B-1)Z² + (A-3B² -2B)Z + (B³+B²-AB) = 0

Above equation can be written as

Z³ + C2.Z² + C1.Z + C0 = 0

Solving Cubic Equation

Cubic equation is solved using following procedure. Calculate Q1, P1 & D.

Q1 = C2.C1/6 - C0/2 - C2³/27
P1 = C2²/9 - C1/3
D = Q1² - P1³

If D >= 0, then equation has only one real root provided by

Z1 = (Q1 + D0.5)1/3 + (Q1 - D0.5)1/3 - C2/3

If D < 0, then equation has 3 real roots, following parameters are calculated

t1 = Q1² / P1³
t2 = (1 - t1)0.5 / t10.5. Q1/abs(Q1)
θ = atan(t2)

Roots are calculated as following -

Z0 = 2.P10.5.cos(θ/3) - C2/3
Z1 = 2.P10.5.cos((θ + 2*Π)/3) - C2/3
Z2 = 2.P10.5.cos((θ + 4*Π)/3) - C2/3

Roots thus calculated are arranged in descending order, highest root gives Z^V and lowest root gives Z^L.

Fugacity

Based on Z^L, liquid fugacity φ_i^L is calculated for each data set.

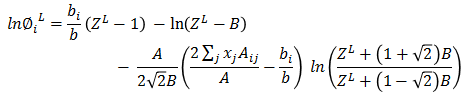
In next step, Vapor phase fugacity is calculated. Mixture properties are estimated as following

a = a1.y1² + 2.a12.y1.y2 + a2.y2²
b = b1.y1 + b2.y2
A = aP/(RT)²
B = bP/RT

Cubic equation is solved as per method shown above to get Z^V.

Z³ + (B-1)Z² + (A-3B² -2B)Z + (B³+B²-AB) = 0

Based on Z^V, vapor fugacity φ_i^V is calculated for each data set.

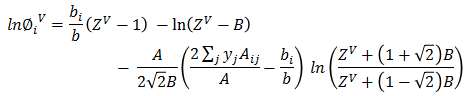
K1 is calculated as:

K1Calculated = φ1L/φ1V

Difference of K1_Experimental and K1_Calculated is obtained for all data points. An objective function is defined as summation of all these differences. Click on Solver in Data Ribbon (Excel 2010) to open dialog box for Solver parameters and input data as shown below.

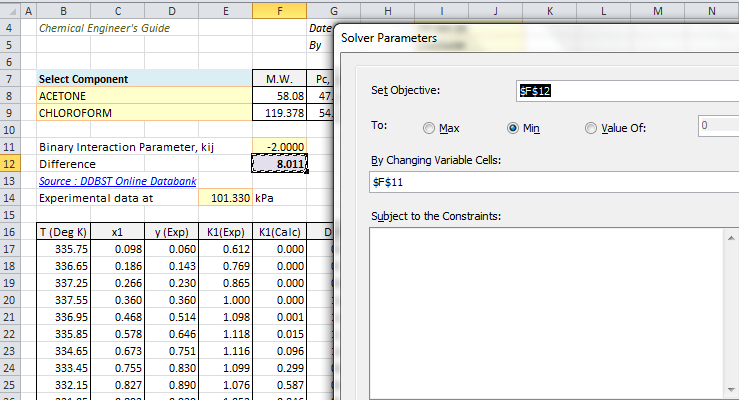
Minimize the objective function by changing values of kij. Uncheck Make Unconstrained Variables Non-Negative, as k12 can take negative value. Click solve to start regression and new value k12 is calculated.

 k12 = -0.0605

Above value is then used to calculate y1 values and results are plotted to check the deviation.

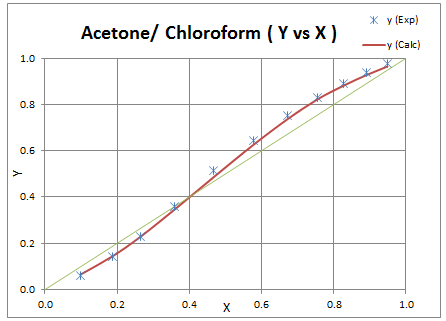
Example

Determine temperature dependent binary interaction parameter used in Peng Robinson EOS ( k12 = k1 + k2.T + k3/T ) for a mixture of acetone and n-Hexane from P x-y experimental data available at 318.15 °K.

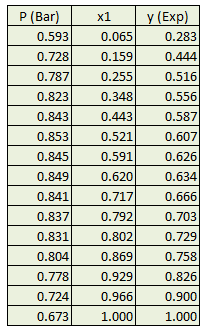
Follow above steps to calculate pure component and mixture parameters. Change formula for kij to make it temperature dependent. As an initial guess put values for 3 parameters (k1,k2,k3) which gives a numeric difference value. In solver select these 3 variables to be varied for minimizing the difference value and then solve it. After doing regression binary interaction parameters are obtained and result is plotted as following.

k1 = -0.0218
k2 = 3.142x10-4
k3 = 10.155

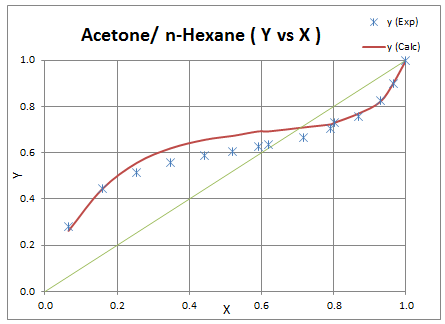
Note : In case of non-convergence, try different initial guess values for kij and then let solver obtain optimized values.

Resources

1. Spreadsheet for Regressing BIP for Peng Robinson EOS