Bubble T flash calculation determine bubble point temperature (T) and vapor mol fraction (Yi) for a mixture at given pressure (P) and liquid mol fraction (Xi). These calculations can be performed in excel spreadsheet using Peng Robinson Equation of State (PR EOS).

Estimate temperature T and vapor mol fraction (Yi). T can be estimated as following -

T = Σ Tisat Xi
Tisat = Tc/[ 1 - 3.ln(P/Pc)/(ln(10).(7 + 7ω)) ]

where Pc, Tc and ω are critical constants for a component i. Vapor mol fraction is estimated as following

Yi = Ki Xi
Ki = exp[ ln(Pc/P) + ln(10)(7/3)(1 + ω )(1-Tc/T)]

First iteration starts with estimated T and Yi. Parameters for Peng Robinson EOS are calculated for each component i.

κi = 0.37464 + 1.54226ω - 0.26992ω²
αi = [ 1 + κi (1 - (T/Tc)0.5)]²
ai = 0.45724 (RTc)²α / Pc
bi = 0.07780 RTc / Pc

Mixture parameters are calculated next

aij = [(ai.aj)0.5(1 - kij)] = aji
a = ΣiΣj aij.Xi.Xj
b = Σi bi.Xi
A = aP/(RT)²
B = bP/RT

where, kij's are Binary Interaction Parameter available from literature.

Following cubic equation is solved to get Z^L.

Z³ + (B-1)Z² + (A-3B² -2B)Z + (B³+B²-AB) = 0

Above equation can be written as

Z³ + C2.Z² + C1.Z + C0 = 0

Solving Cubic Equation

Cubic equation is solved using following procedure. Calculate Q1, P1 & D.

Q1 = C2.C1/6 - C0/2 - C2³/27
P1 = C2²/9 - C1/3
D = Q1² - P1³

If D >= 0, then equation has only one real root provided by

Z1 = (Q1 + D0.5)1/3 + (Q1 - D0.5)1/3 - C2/3

If D < 0, then equation has 3 real roots, following parameters are calculated

t1 = Q1² / P1³
t2 = (1 - t1)0.5 / t10.5. Q1/abs(Q1)
θ = atan(t2)

Roots are calculated as following -

Z0 = 2.P10.5.cos(θ/3) - C2/3
Z1 = 2.P10.5.cos((θ + 2*Π)/3) - C2/3
Z2 = 2.P10.5.cos((θ + 4*Π)/3) - C2/3

Roots thus calculated are arranged in descending order, highest root gives Z^V and lowest root gives Z^L.

Fugacity

Based on Z^L, liquid fugacity φ_i^L is calculated for each component.

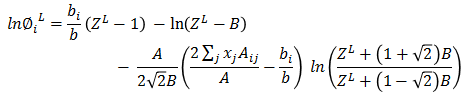
As a next step, Vapor phase fugacity is calculated. Mixture properties are estimated as following -

a = ΣiΣj aij.Yi.Yj
b = Σi bi.Yi
A = aP/(RT)²
B = bP/RT

Cubic equation is solved as per method shown above to get Z^V.

Z³ + (B-1)Z² + (A-3B² -2B)Z + (B³+B²-AB) = 0

Based on Z^V, vapor fugacity φ_i^V is calculated for each component.

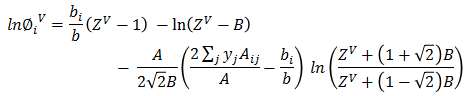
Vapor phase mol fraction is calculated as

Yi = Xi.φiL/φiV

New values of Yi thus calculated are again used to estimate φ_i^V and thereafter Yi. This iteration is repeated till there is no further change in Yi values. Typically, in 25 iterations change in Yi values become negligible.

At the end of iteration ΣYi is calculated, if it is close to 1, results are obtained. If not, new value of T is estimated such that ΣYi is close to 1. In excel it can be achieved by using GOAL SEEK function, in which T value is changed to make summation equal to 1.

Note

For some initial values of Temperature, Yi become equal to Xi and summation ΣYi becomes 1, it happens when initial guess for T falls in critical region. For such cases use different value of temperature, such that summation is not equal to 1 and then use Excel GOAL SEEK function to estimate Bubble Point Temperature and vapor mol fractions Yi.

Resources

1. Spreadsheet for Bubble T Flash using PR EOS