Bingham plastic is a material that behaves as rigid body at low stresses but flows as a viscous fluid at high stress. This behaviour is exhibited by slurries, suspensions of solids in liquids, paints, emulsions, foams, etc.

Bingham model is described by following relation.

τ = τo + μp γ

where, τ is shear stress, γ is shear rate, τo is called minimum yield stress and μp is called plastic viscosity.

Reynolds number for Bingham plastic fluid is defined as

Re = D V ρ / μp

where, D is pipe inside diameter, V is fluid velocity and ρ is fluid density.

For Laminar flow, friction factor is provided by Buckingham Reiner equation.

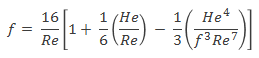
where, He is Hedstrom number and is calculated as

He = D²ρτo / μp²

For turbulent flow, an empirical relationship was developed by Darby and Melson.

The friction factor for a Bingham plastic can be calculated for any Reynolds number from the equation.

f = ( fLm + fTm ) 1/m

where, fL is laminar flow friction factor and fT is turbulent flow friction factor. Factor m is calculated from following equation.

m = 1.7 + 40,000 / Re

Pressure drop is calculated as

ΔP = 2fρV² (L'/D)

L' = L + Le

where, L is the pipe length and Le is equivalent length due to loss in pipe fittings and is calculated as

Le = kD / 4f

Resources

1. Web based calculation available at checalc.com
2. Spreadsheet for Bingham Plastic Fluid

References

1. Bingham plastic at Wikipedia
2. Fluid friction at Petrowiki
3. Chemical Engineering Fluid Mechanics, Ron Darby, 2^nd Edition