This article shows how to prepare Pxy and Txy diagram for binary mixtures in excel spreadsheet based on Wilson, NRTL and UNIQUAC activity coefficient model.

For low to moderate pressure vapor liquid equilibrium (VLE) is described by modified Raoult's Law -

 yi P = xi γi Pisat

where, y_i is vapor mol fraction, P is system pressure, x_i is liquid mol fraction, γ_i is activity coefficient and P_i^sat is vapor pressure for a pure component i. Vapor pressure is calculated based on Antoine equation.

ln Pisat = Ai - Bi /( T + Ci )

A_i , B_i and C_i are Antoine equation constants and T is temperature at which vapor pressure is to be calculated.

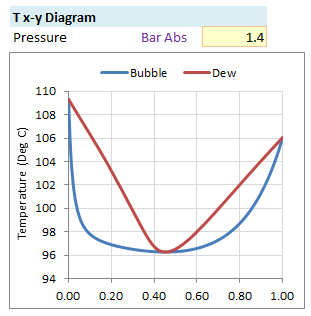
Txy Diagram

Txy diagram plots bubble and dew point curves at constant pressure P. Put down the liquid mol fraction x₁ from 0.0 to 1.0 with increment of 0.01 in spreadsheet. Iteration is done for each liquid mol fraction to estimate equilibrium temperature T and activity coefficient γ_i.

For first iteration, T₁^sat and T₂^sat are calculated from Antoine equation.

Tisat = Bi/ (Ai - ln Pisat) - Ci

Equilibrium temperature is estimated as following -

T = x1 T1sat + (1 - x1)T2sat 

Based on temperature T, activity coefficient γ₁ and γ₂ are calculated from activity coefficient model selected e.g. Wilson, NRTL and UNIQUAC. For ideal mixture γ₁ and γ₂ are 1.

Saturation pressure for a component is calculated using following equation -

P1sat = P/(x1γ1 +(1-x1)γ2 P2sat/P1sat)

Temperature corresponding to the vapor pressure P₁^sat is calculated from Antoine equation.

T = B1/ (A1 - ln P1sat) - C1

Temperatue thus calculated is used for next iteration and activity coefficients γ₁ and γ₂ are calculated. Iterations are repeated till there is no change in subsequent temperature estimations. Typically temperature difference becomes negligible within 10 iterations.

Above steps are repeated for all liquid mol fractions, thereby giving a table of x₁ and corresponding temperature T. Vapor mol fraction y₁ is calculated as following -

y1 = x1 γ1 P1sat/ P

Plot of T, x₁ & y₁ gives Txy Diagram -

Pxy Diagram

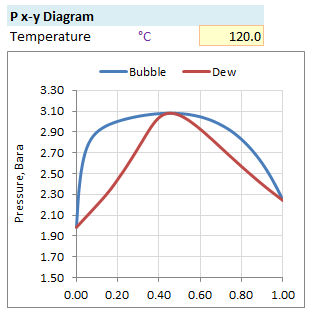
Pxy diagram plots bubble and dew point curves at constant temperature T. Put down the liquid mol fraction x₁ from 0.0 to 1.0 with increment of 0.01 in spreadsheet. Calculate activity coefficients γ₁ and γ₂ based on activity coefficient model selected from Wilson, NRTL and UNIQUAC.

Calculate partial pressure of each component P₁ and P₂ as following -

P1 = x1 γ1 P1sat
P2 = (1 - x1) γ2 P2sat

Equilibrium pressure is obtained as following -

P = P1 + P2

Vapor mol fraction is calculated as per below equation.

y1 = P1 / P

Plot of P, x₁ & y₁ gives Pxy Diagram -

Wilson Model

Activity coefficient for binary system are defined as -

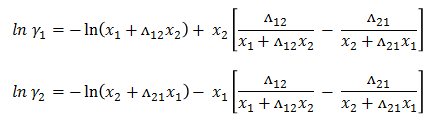
Wilson parameter is provided by following equation -

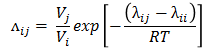
where, λ₁₂ - λ₁₁ and λ₂₁ - λ₂₂ are binary interaction parameters available from literature for a binary pair.

Modified Rackett equation is used to estimate liquid molar volume V₁ & V₂.

V = (RTc/Pc)ZRA [1 + (1-Tr)^(2/7)]

where, T_c and P_c are critical temperature and pressure. T_r is the reduced temperature. Z_RA is Rackett equation parameter, if it is not available, it can be estimated from accentric factor ω as following.

ZRA = 0.29056 - 0.08775ω

NRTL Model

Activity coefficient for binary system are defined as -

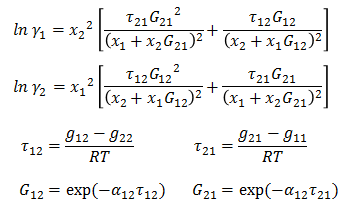
Parameter g₁₂ - g₂₂ and g₂₁ - g₁₁ are binary parameters available from literature. α₁₂ is related to non-randomness in mixture and is available from literature for binary pairs.

UNIQUAC Model

Activity coefficient for binary system are defined as -

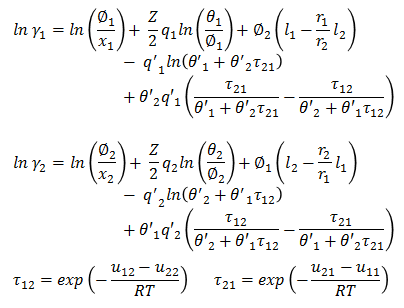
Parameter u₁₂ - u₂₂ and u₂₁ - u₁₁ are binary parameters available from literature. Remaining parameters are calculated as following -

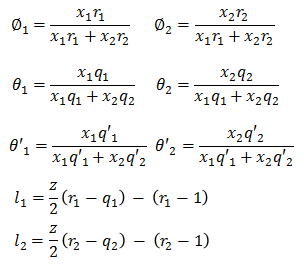
where z is set equal to 10 and r, q & q' are pure component UNIQUAC parameters.

Resources

1. Spreadsheet for Binary Vapor Liquid Equilibrium